Fun with magic hashes in Python
Over the past three months, I took part in the Kaggle Code Golf competition as part of jailctf merger. The event recently ended, and to our surprise, we ended up taking second place and walking away with a $20,000 prize 🤑.
If you’ve never heard of code golf, it’s a kind of recreational sport where you try to solve a programming task in as few bytes as possible. Despite being a silly exercise, I think it promotes a really interesting combination of algorithms, math, and cursed language tricks.
Throughout the competition, we had to golf 400 grid-based problems in Python, all sourced from the ARC-AGI v1 dataset. In this post, I want to talk about my favourite task, Task 48, which I solved using a technique called magic hashing. With it, I managed to obtain the leading 92-byte solution, later improved to 91 bytes after some post-mortem discussions with other teams.
This post serves as both an introduction to magic hashing techniques, and a detailed breakdown of the ideas and optimizations that made Task 48 an interesting problem to crack.
Setup#
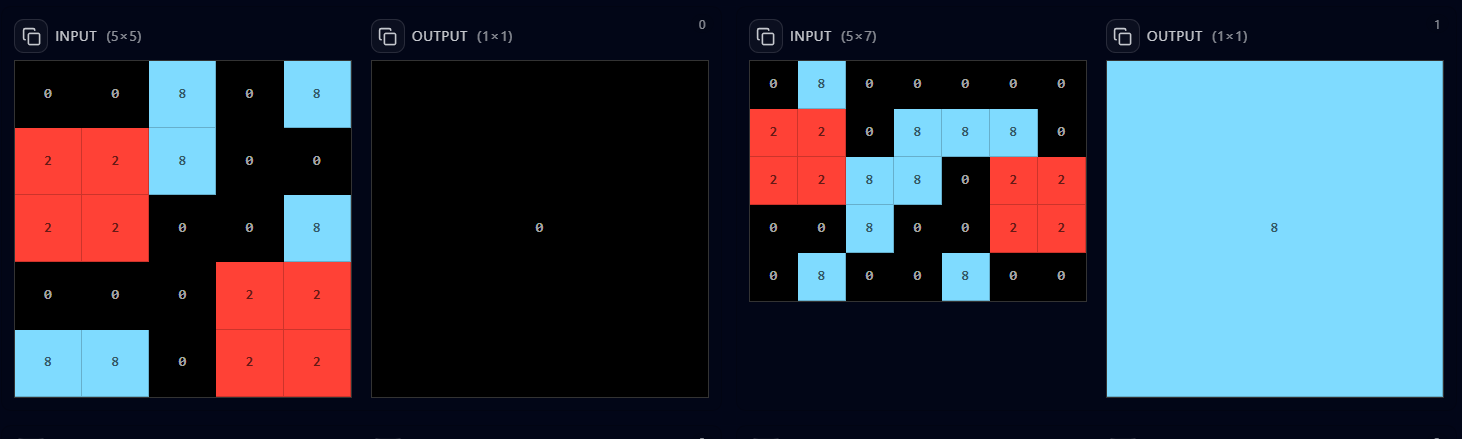
Example grid for Task 48
Problem: Given an input grid consisting of black (0), red (2) and cyan (8),
determine whether there is a cyan path connecting the two red blocks through a series of
adjacent connections.
Output: A 1x1 grid that is cyan if a path exists, and black otherwise.
In this competition, all of the solutions were written in Python, and each submission
had to define a function p(g) that accepts an input grid g and returns the
corresponding output grid, e.g.
task048.py
p=lambda g:...At first glance, this looks like a standard pathfinding task.
But two details that make this problem interesting:
- The output is binary, either
0or8 - The server validates the solution against 270 fixed test cases
Since there are only two possible outputs and a fixed number of test cases, it can actually be solved by hardcoding shorter than it can be solved legit. But to hardcode it efficiently, we’ll need to use a magic hash.
Magic hashing#
Suppose we want a formula that maps:
1 -> 3
2 -> 4
3 -> 1
The straightforward approach is to use a lookup table like [0,3,4,1][x]. It works,
but it’s not particularly short.
Instead, we should look for an arithmetic expression that happens to yield the correct
mapping. This is the optimal 6-byte expression: 4+9%~x.
Finding magic formulae like this manually is possible, but quickly becomes infeasible with more inputs. To find the one above, I used a tool called pysearch – a Rust program that bruteforces the optimal expression by enumerating expression trees. For expressions up to around length 13-14, pysearch can usually find the optimal arithmetic expression within several minutes. It’s an extremely useful tool that we relied on a lot during the competition, in at least 25% of the tasks.
However, even pysearch struggles when the solution space is too large. Consider this example:
51 -> 56
42 -> 29
78 -> 31
16 -> 41
20 -> 22
21 -> 3
I randomly wrote down these numbers, but pysearch would take far too long to find a solution here. This is where magic hashing comes in.
Instead of searching for a direct mapping, we find a perfect (or near-perfect) hash function that maps each input to a unique value within a small range, and then index that value in a lookup table.
Let’s write a script that bruteforces all possible collision-free hash
functions of the form x%a%b:
find_perfect_hash.py
inputs = [51, 42, 78, 16, 20, 21]
n = 1 << 99
for a in range(1, 100):
for b in range(1, 100):
h = [x % a % b for x in inputs]
if len(h) == len(set(h)) and max(h) < n:
n = max(h)
print(f'{a} {b}: {h} ({n=})')This finds two candidates:
8 7: [3, 2, 6, 0, 4, 5] (n=6)
53 8: [3, 2, 1, 0, 4, 5] (n=5)
The first is a near-perfect hash (with a hole at index 1), while the second is a perfect hash. We can use this to construct a 26-byte magic hash:
[41,31,29,56,22,3][x%53%8]
However, since all values are within ASCII range, we can shorten it to 17 bytes by replacing the list with a byte string (raw bytes are shown as escapes):
b')\x1f\x1d8\x16\x03'[x%53%8]
Alternatively, a bitmask lookup table works but ends up longer at 23 bytes:
3605125097>>x%53%8*6&63
These are the most common forms of a magic hash: combining a modulo chain with a lookup
table. Note that the hash function doesn’t necessarily have to be a modulo chain,
so long as it maps the inputs into a sufficiently small range with zero collisions.
In practice, other constructions like a//x%b, a%x%b and x*a%b%c can also be effective
hash functions that are short, yet random enough to minimize the probability of a collision.
Usually, you can also use pysearch to brute force such a hash function by
modifying fn match_all(expr: &Expr) in params.rs with a custom predicate.
Task 48#
Returning to the original problem – can we apply these ideas of magic hashing to Task 48?
Unfortunately, the idea falls apart when we have this many inputs. The odds of having zero collisions for a perfect hash function across 270 inputs is \( \frac{270!}{270^{270}} \approx 2 \cdot 10^{-116} \), which is vanishingly small. What this means is we should expect to brute force \( 2 \cdot 10^{116} \) hash functions before finding one that works. Even a near-perfect hash is extremely unlikely due to the birthday paradox.
Let’s reframe the problem. We’re looking for a function f(g) that produces the correct
binary outputs for all inputs. Assuming f is essentially random, the probability it’s
correct is \( 2^{-270} \).
Now suppose that f accepts some seed as an additional parameter, which influences
f deterministically in some way. Then, on average, there should exist a
270-bit seed such that f(g, seed) produces the correct mapping on all test cases.
Conveniently, Python has a built-in hash() function we can use. Although strings
don’t hash deterministically in Python 3 due to DDoS prevention, other objects like tuples
and integers do! In relatively recent Python versions, hash() will return these
exact values every single time:
>>> hash(42)
42
>>> hash(1.0)
1
>>> hash(1.5)
1152921504606846977
>>> hash((1, 2, 3))
529344067295497451
To use this approach, we need to convert g into a tuple. The shortest known
solution here takes 17 bytes:
hash(tuple(str(g).encode())) # 28b
hash((*str(g).encode(),)) # 25b
hash((*sum(g,[]),)) # 19b
hash((*b'%r'%g,)) # 17b
Combining this with the seed idea, we can imagine that something like this works:
task048.py
p=lambda g:[[hash((*b'insert_really_long_seed_here%r'%g,))%2*8]]With 270 bits of information, the seed itself needs to be at least \( \lceil\frac{270}{7}\rceil=39 \)
bytes, which equates to a 75-byte solution (73 if we replace %2*8 with &8). The problem is it’s
not actually computable in practice since we would need to brute force \( 2^{270} \) different
seeds. In addition, the tuple_hash implementation
in CPython internally uses an algorithm called xxHash.
Although it is a non-cryptographic hash, it is complex enough that the seed cannot be
determined faster than brute force (to the best of my knowledge).
A new approach#
This poses an interesting question: does there exist some hash function for which we can determine a magic seed in polynomial time?
Surprisingly, the answer is yes!
Let’s revisit the example from earlier, which I’ll rewrite in function notation:
f(51, seed) = 29
f(42, seed) = 31
f(78, seed) = 31
f(16, seed) = 41
f(20, seed) = 22
f(21, seed) = 3
Here, f is some hash function, and seed is an unknown quantity that satisfies these
equations. Let’s encode each input as a 6-element vector. The actual algorithm to convert
the inputs into vectors needs to be something deterministic but “random-looking”. One
way is to use modular exponentiation:
lambda x: [x**i%61 for i in range(1, 7)]
Using this encoding generates a somewhat random sequence for each input:
f([51, 39, 37, 57, 40, 27], seed) = 56
f([42, 56, 34, 25, 13, 58], seed) = 29
f([17, 45, 33, 12, 21, 52], seed) = 31
f([16, 12, 9, 22, 47, 20], seed) = 41
f([20, 34, 9, 58, 1, 20], seed) = 22
f([21, 14, 50, 13, 29, 60], seed) = 3
Here is the key insight: if we define f as the dot product of the input vector and
seed vector, then finding the seed becomes a linear algebra problem:
$$ \begin{pmatrix} 51 & 39 & 37 & 57 & 40 & 27 \\ 42 & 56 & 34 & 25 & 13 & 58 \\ 17 & 45 & 33 & 12 & 21 & 52 \\ 16 & 12 & 9 & 22 & 47 & 20 \\ 20 & 34 & 9 & 58 & 1 & 20 \\ 21 & 14 & 50 & 13 & 29 & 60 \end{pmatrix} \cdot \begin{pmatrix} \text{seed[0]} \\ \text{seed[1]} \\ \text{seed[2]} \\ \text{seed[3]} \\ \text{seed[4]} \\ \text{seed[5]} \end{pmatrix} = \begin{pmatrix} 56 \\ 29 \\ 31 \\ 41 \\ 22 \\ 3 \end{pmatrix} $$
We can also write it down as a list of 6 equations and 6 unknowns:
51*seed[0] + 39*seed[1] + 37*seed[2] + 57*seed[3] + 40*seed[4] + 27*seed[5] = 56
42*seed[0] + 56*seed[1] + 34*seed[2] + 25*seed[3] + 13*seed[4] + 58*seed[5] = 29
17*seed[0] + 45*seed[1] + 33*seed[2] + 12*seed[3] + 21*seed[4] + 52*seed[5] = 31
16*seed[0] + 12*seed[1] + 9*seed[2] + 22*seed[3] + 47*seed[4] + 20*seed[5] = 41
20*seed[0] + 34*seed[1] + 9*seed[2] + 58*seed[3] + 1*seed[4] + 20*seed[5] = 22
21*seed[0] + 14*seed[1] + 50*seed[2] + 13*seed[3] + 29*seed[4] + 60*seed[5] = 3
Because this is a linear system, we can easily find a solution to seed in
\( \mathcal{O}(n^3) \) time via
Gaussian elimination.
The catch is that seed is not necessarily integer-valued. We can fix this by working
modulo \( p \) instead of over the integers. As long as \( p \) is prime, Gaussian elimination
still works thanks to the properties of finite fields. I’ll choose \( p = 59 \), the
smallest prime greater than the maximum target value.
After solving the system, the resulting seed is [2, 33, 51, 22, 40, 46].
A direct implementation looks like this:
sum(x**(i+1)%61*b'\x02!3\x16(.'[i]for i in range(6))%59
Interestingly, this idea was independently discovered by CGSE user @ais523 a couple of years ago. Despite this, it doesn’t appear to be a very well-known trick because I haven’t seen any other posts about it online.
First attempt#
Applying this idea to Task 48, we want to use \( p = 2 \), which actually simplifies things
because we can directly compute a binary dot product using (x&y).bit_count()%2, assuming
the vector bits are represented as a binary number. The only challenge left
is how to store the 270-bit seed compactly.
My approach was to pack the seed into 7-bit chunks so it fits neatly in a byte string,
and then sum up the results (using g:=hash((*b'%r'%g,)) to generate random numbers for
the input vector):
task048.py
p=lambda g:[[sum((c&(g:=hash((*b'%r'%g,)))).bit_count()for c in b'VL\x12\x0e\x02OS2\x15\x05%Rvi}ID\x17\x1dvw>H(\x1a\x0bcg\x7fH:\x183x?-x,R')%2*8]]In total, this comes out to 113 bytes – not bad.
At the time, this beat the best entry on the community spreadsheet, so I thought I was close to optimal. But to my surprise, @4atj posted a 97 a few days later, so my solution clearly had plenty of room for improvement.
Back to the drawing board#
I knew there was a lot of overhead in my current solution from looping over characters and computing bit counts, but I couldn’t see any obvious way to eliminate them. We needed to take a fundamentally different approach.
Frustrated, I went back to stare at the hash() template I had written earlier:
p=lambda g:[[hash((*b'insert_really_long_seed_here%r'%g,))&8]]
This approach takes too long to compute, but maybe we can optimize it.
Then, I had an idea: what if instead of one massive seed, we split the inputs into buckets and solve for several smaller seeds independently?
p=lambda g:[[hash((*b'AAA BBB ... MMM'.split()[h(g)%13]+b'%r'%g,))&8]]
Here, h(g)%13 is some hash function that buckets the 270 inputs into 13 roughly equal parts.
Each bucket requires \( \frac{270}{13} \approx 20.77 \) bits of information.
At 7 bits per byte, we should expect a 3-byte seed per bucket.
The .split() is really long, but we can shorten it with some clever slicing:
p=lambda g:[[hash((*b'AAABBB...MMM'[h(g)%13*3:][:3]+b'%r'%g,))&8]]
But this only leaves 9 bytes left for the hash function (to tie 97), and there is a catch:
with exactly 3 bytes allocated per bucket, we need h(g)%13 to distribute the inputs
almost perfectly across the buckets. If any bucket gets significantly more than 21 inputs,
a valid 3-byte seed likely doesn’t exist.
We need to choose the hash function carefully. The shortest way to hash g into an
integer is sum(b'%r'%g), but its input distribution modulo 13 is uneven:
hist = [24, 30, 18, 24, 21, 21, 25, 14, 19, 24, 15, 22, 13]
A better approach might be to use hash((*'???%r'%g,)) and brute force a seed with a better
distribution. But this still seemed too long, so I was clearly missing some other
trick.
After staring at the code a bit longer, I realized we could actually drop the [:3]:
p=lambda g:[[hash((*b'AAABBB...MMM'[h(g)%13*3:]+b'%r'%g,))&8]]
p=lambda g:[[hash((*b'AAABBB...MMM%r'[h(g)%13*3:]%g,))&8]] # merge %r with str
Even though the buckets now “overlap”, it still works! The seed for the
current bucket includes the seeds for all the buckets after it. When we compute the seed for
bucket 12 (the MMM part), the seed for bucket 11 becomes a 6-byte seed whose suffix is
bucket 12’s seed. Likewise, the seed for bucket 10 becomes a 9-byte seed whose suffix is the concatenation of bucket 11 and 12’s seeds – and so on.
We can therefore compute the entire seed with a depth-first search starting from the last bucket.
For each seed we obtain for bucket i, we can fix that and then move on to bucket i-1
until we reach bucket 0.
Finally, this new idea led to a 99-byte solution:
p=lambda g:[[hash((x:=hash((4,*b'%r'%g)),*b"z{Y!D\x01T\x03ehJ~\x1c\x0fg9'2|\x02Ro{\x15\x1d\x08M)p\x1c`z\\8T=*\x1d\x19"[x%13*3:]))&8]]
The code structure is slightly different, but the idea is the same. However, the hash
function uses hash instead of sum because I could not get a good enough distribution
with sum, even though it is shorter.
The 92-byte solution#
Because of this my solution was suboptimal, but it didn’t end up mattering because I immediately found a save that brought it down to 92 bytes:
p=lambda g:[[hash((*b'+]\x13`d\x1aB\x14Px <Ia\x15AacF#\x10p3e7"\x10kz\x1e0\x02\x0cW}k&N\x0f%r'[sum(b'\x1c%r'%g)%39:]%g,))&8]]
In fact, all I did was re-run the bruteforcer script with mod=39 instead of mod=13.
It found a solution rather quickly using sum this time.
It’s not entirely obvious why it works, so let’s do a quick analysis.
The bucket hash, sum(b'\x1c%r'%g)%39, has the following distribution:
hist = [11, 5, 8, 7, 11, 12, 3, 7, 11, 11, 6, 9, 6, 7, 2, 6, 15, 6, 6, 5,
7, 8, 0, 7, 10, 8, 4, 6, 10, 8, 1, 6, 13, 7, 6, 3, 6, 5, 1]
Because we are using %39, each bucket represents a 1-byte seed to brute force.
Recall that hist[i] is the number of inputs that hash into bucket i. For each bucket,
we can brute force 128 possibilities for the 1-byte seed (124 if we ignore \0, \r,
\n and %).
For a bucket with \( n \) inputs, the probability that a given random 1-byte seed satisfies all \( n \) inputs is \( 2^{-n} \). Since we have \( 2^7 \) seeds to choose from, the expected number of working seeds is \( 2^{7-n} \).
However, the seed for each bucket includes the seeds of all the buckets after it, so
to know the expected number of seeds that work when we get to index i, we
need to calculate the cumulative count:
>>> expected_seeds = [2**sum(7 - x for x in hist[i:]) for i in range(len(hist))]
>>> expected_seeds
[8, 128, 32, 64, 64, 1024, 32768, 2048, 2048, 32768, 524288, 262144, 1048576,
524288, 524288, 16384, 8192, 2097152, 1048576, 524288, 131072, 131072, 262144,
2048, 2048, 16384, 32768, 4096, 2048, 16384, 32768, 512, 256, 16384, 16384, 8192,
512, 256, 64]
All of the values are above 1, so we are very likely to find a solution!
The question of how long it takes to find a solution based on the distribution is more difficult to answer, but empirically the 92-byte solution took less than an hour, which was good enough for me :)
Post-mortem#
After the competition, Code Golf Interntional shared their 95-byte solution:
task048_cgi.py
p=lambda g:[[(o:=hash((*b"'%a3byQ"%g,)))//b'Y(_4\x19Lha\x7fcy\x0617vZ4%_R\x19|K~~,|\x04~(xs2E,]{'[o%37]%-3&8]]Their approach is quite different but uses a similar bucketing strategy, which involved a second lookup table outside of the hash function.
One thing that I missed was how they used %-3&8 instead of &8. Although it is 3
bytes longer, the distribution returns 8 \( 66\% \) of the time,
whereas &8 is only \( 50\% \).
If we compare this to the distribution of the actual test cases, 186 out of 270 of the
answers are 8, which is \( 68.9\% \).
Because the distribution matches more closely to the actual distribution, the seed length will be shorter, on average. We can verify this mathematically:
>>> from math import log2
>>> p = 186/270
>>> f = lambda q: q**p * (1-q)**(1-p)
>>> log2(1/f(1/2)**270) / 7
38.57142857142857
>>> log2(1/f(2/3)**270) / 7
34.56283931353031
The calculation shows we only need 35 bytes for the seed instead of 39, which saves 1 more byte:
task048.py
# 91b (post mortem)
p=lambda g:[[hash((*b'`\x16_e\x01L\x16\x07\x170Q\x1f<7M\x1c\x14bK9\x11"`@\x12t\x0fzn!&\x0ca"V%r'[sum(b'\t%r'%g)%33:]%g,))%-3&8]]Nov. 13 update#
Another 2 byte improvement was found by @HPWiz:
task048.py
# 89b (post mortem, HPWiz)
p=lambda g:[[hash((*(x:=b"S\x10\x13`'yT\x10ZFQ\x13GEb1'\x05\x1bO~\x03V{m\x13\\P~#{\x01w$%r!"%g)[sum(x)%33:],))%-3&8]]Since we’re already using b'...%r'%g for the seed string, we can also reuse it in the
sum! The sum will be offset by some constant modulo 33 because of the extra seed
characters, but if we brute force enough times, the offset will be exactly 0 and
so we can just do: (x:=b'...%r'%g)[sum(x)%33:].
Conclusion#
If you enjoyed this writeup, I highly recommend eyepopslikeamosquito’s old golf articles on PerlMonks:
- The 10**21 problem
- The golf course looks great, my swing feels good, I like my chances
- Drunk on golf: 99 Bottles of Beer
- Compression in Golf
Also shoutout to @helloperson. for carrying in the final month of the competition.